発達障害の可能性のある児童生徒等に対する
教科指導法研究事業

④算数・数学における「志導」に関する教授法(1)

★　対象とした学習上のつまずくポイント1（A　数と計算）

　「ものとものとを対応させることによって、ものの個数を比べること」について、数を正しく数える（計数）ためには、以下に示す5つの原理を理解する必要がある。

• ● 一対一対応：1つのモノに数の名前を1つだけ割り当てるという原理
• ● 安定した順序：用いられる数詞が常に同じ順序で配列される原理
• ● 基数性：最後の数が集合の数の大きさを示すという原理
• ● 順序無関連：数える順序は関係がないという原理
• ● 抽象性：数えるものがなんであろうと全く関係がないという原理

　このうち、継次処理型学習者は、一対一対応と安定した順序の理解は容易だが、基数性の理解につまずきが生じやすい。一方、同時処理型学習者は、基数性・順序無関連・抽象性の理解は容易だが、安定した順序の理解につまずきが生じやすい。

★　上記に対する取組内容１（A　数と計算）

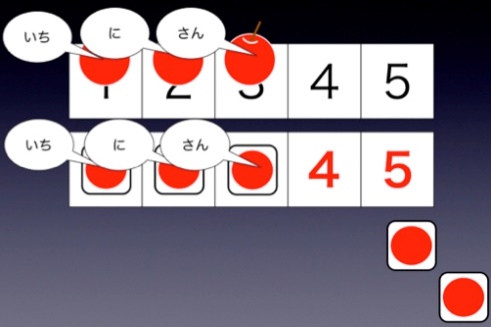
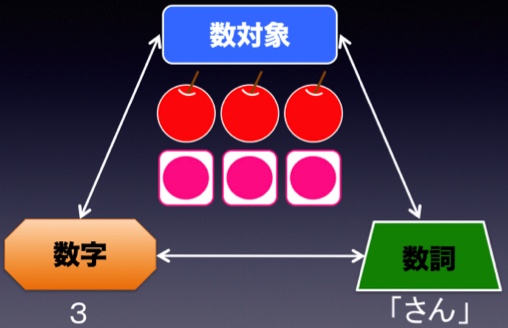
　数概念を獲得するためには、図7に示す三項関係の理解が重要になる。その上で、一対一対応、安定した順序、基数性、順序無関連、抽象性を学習することで正確に計数できるようになる。この際、数対象が具体物であれ半具体物（数図ブロック）であれ、一つの数対象に、一つの数字・数詞を割り当てる練習をする必要があり、図8に示すように、具体物と半具体物を同じ数字パネルに、一つの数詞を言いながら、対応する数字のパネルに置いて理解を促す。継次処理型学習者の場合は、特に数詞を強調しながら、同時処理型学習者の場合には、特に数字を強調しながら、児童生徒に関わる。この方法により、一対一対応、安定した順序が習得できるとともに、最後に唱えた数詞・数対象が置かれた数字が集合数であること（基数性）の理解につながる。